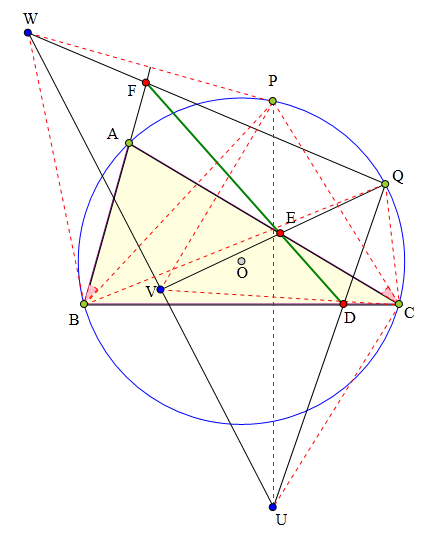
526 证明题:
△ABC内接于⊙O,
P、Q为⊙O上另外两点,
P、U关于BC对称,
QU交BC于D,
P、V关于AC对称,
QV交AC于E,
P、W关于AB对称,
QW交AB于F,
求证:
D、E、F三点共线
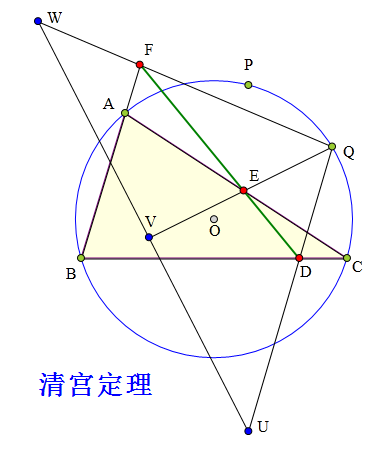
<解法 1:>
连接PB、PC、VC、QC、QB、UC、BW,
∵点P和V关于CA对称
∴∠PCV=2∠PCA
同理∠PBW=2∠PBA
∵∠PCA=∠PBA
∴∠PCV=∠PBW
∵∠PCQ=∠PBQ
∴∠PCV+∠PCQ=∠PBW+∠PBQ
∴∠QCV=∠QBW
∴△QCV和△QBW有一个顶角相等,
∴S△QCV/S△QBW =(CV·CQ)/(BW·BQ)
∵CV=CP,BW=BP,
∴S△QCV/S△QBW=(CP·CQ)/(BP·BQ)
同理S△QAW/S△QCU=(AP·AQ)/(CP·CQ)
S△QBU/S△QAV=(BP·BQ)/(AP·AQ)
∴(BD/DC)·(CE/EA)·(AF/FB)
=[S△QBU/S△QCU]·[S△QCV/S△QAV]·[S△QAW/S△QBW]
=[S△QBU/S△QAV]·[S△QCV/S△QBW]·[S△QAW/S△QCU]
=[(BP·BQ)/(AP·AQ)]·[(CP·CQ)/(BP·BQ)]· [(AP·AQ)/(CP·CQ)] =1
根据梅涅劳斯定理的逆定理,
D、E、F三点在同一直线上