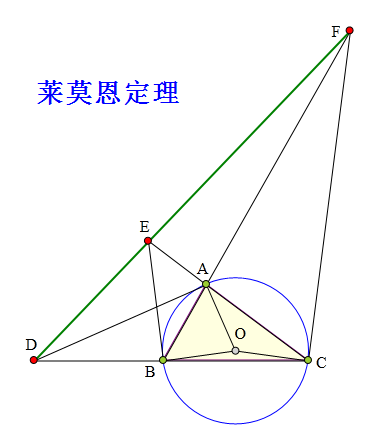
525 证明题:
△ABC内接于⊙O,
AD丄OA交BC于D,
BE丄OB交AC于E,
CF丄OC交AB于F,
求证:
D、E、F三点共线
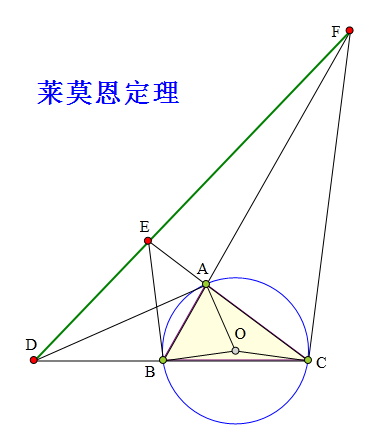
<解法 1:>
由弦切角定理可以得到:
sin∠ACF=sin∠ABC
sin∠BCF=sin∠BAC
sin∠BAD=sin∠BCA
sin∠CAD=sin∠ABC
sin∠CBE=sin∠BAC
sin∠ABE=sin∠BCA
所以,我们可以得到:
(sin∠ACF/sin∠BCF)·(sin∠BAD/sin∠CAD)·(sin∠CBE/sin∠ABE)=1,
这是角元形式的梅涅劳斯定理,
∴△ABC被直线DEF所截,
∴D、E、F共线。