522 证明题:
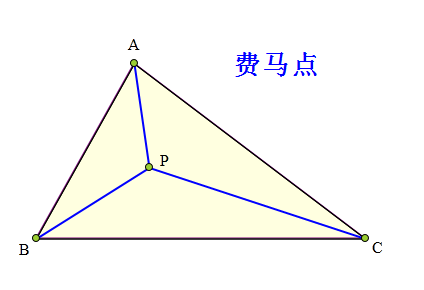
△ABC中,
各内角都小于120°,
P为△ABC内一点,
L=PA+PB+PC。
求证:
当∠APB=∠APC=120°时,
L的值最小
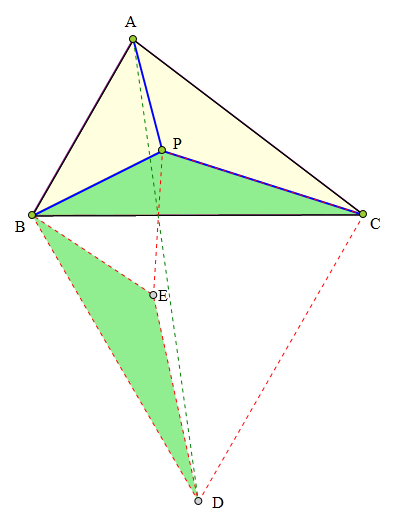
<解法 1:>
以BC为边作正△BCD,
以BP为边作正△BPE,
连接PE、ED。
∵∠PBE=∠CBD=60°
∴∠PBC=∠EBD
∴△BPC≌△BED
∴PC=DE
∴L=PA+PE+ED。
当A、P、E、D共线时,L最短。
∵A、P、E、D共线
∴∠APB=180°-60°=120°
∴∠BED=180°-60°=∠BPC=120°
故得证