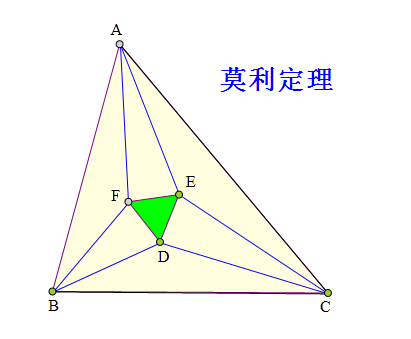
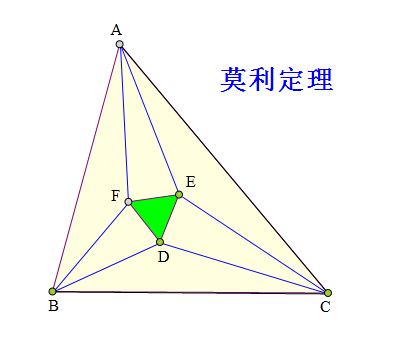
D、E、F为△ABC内三点且:
∠CAE=∠FAE=∠BAF，
∠ABF=∠FBD=∠DBC，
∠BCD=∠DCE=∠ECA，
求证：
△DEF为正三角形

设∠A=3α，∠B=3β，∠C=3γ，
则:α+β+γ = 60°
∵AE：AC=sinγ：sin(α+γ)
AF：AB=sinβ：sin(α+β) ，
AB：AC=sin3γ：sin3β，
∴AE:AF=
(ACsinγ/sin(α+γ))：(ABsinβ/sin(α+β))，
而sin3γ：sin3β=
(sinγ·sin(60°+γ)·sin(60°-γ) )：(sinβ·sin(60°+β)·sin(60°-β))，
sin(α+β)·sin(60°-β)=sin(α+γ)·sin(60°-γ)，
∴AE：AF=sin(60°+β)：sin(60°+γ)，
∴在△AEF中，∠AEF=60°+γ，
同理∠CED=60°+α，
∴∠DEF=60°，
同理∠DFE=60°，
∴△DEF为正三角形。