516 证明题:
ABCDEF为⊙O的外切六边形,
求证:
AD、BE、CF交于一点。
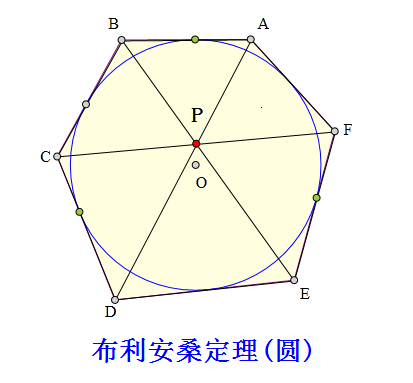
<解法 1:>
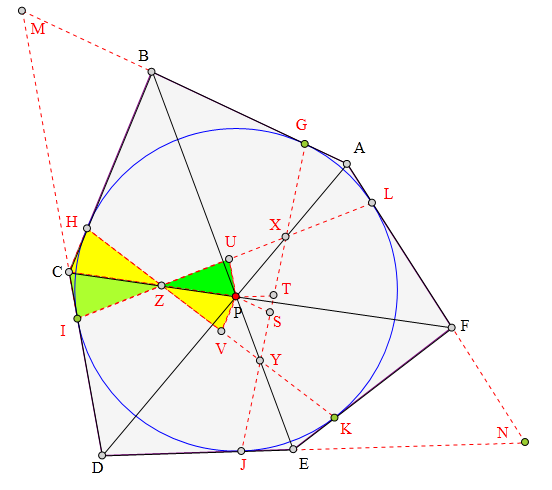
延长AB、CD交于M,
延长AF、DE交于N,
则AMDN为圆外切四边形,
由牛顿定理得:
AD、GJ、IL三点共线,设为X。
同理可证:
BE、GJ、HK三点共线,设为Y。
CF、HK、IL三点共线,设为Z。
由弦切角定理易得∠BGJ=∠DJG,
作PS//AB交GJ于S,PT//DE交GJ于T,
则∠PTS=180°-∠DJG=180°-∠BGJ=∠PST,
所以PT=PS,
作PU//CD交LI于U,又因为PT//DE,
则PU/ID=XP/XD=PT/DJ,
由切线长定理知ID=DJ,
所以PU=PT,
作PV//BC交HK于V,
同理可证PV=PS,
所以PU=PT=PS=PV,
因为PU//CI,
所以PC被IU分成的两段之比为PU/CI,
因为PV//CH,
所以PC被HV分成的两段之比为PV/CH,
又因为PU=PV(已证),CI=CH,
所以PU/CI=PV/CH,
即IU、PC的交点与HV、PC的交点重合,
所以IU、PC、HV共点,
又因为CF、HK、IL共点(已证),
所以C、P、F共线,
即AD、BE、CF共点
<解法 2:>
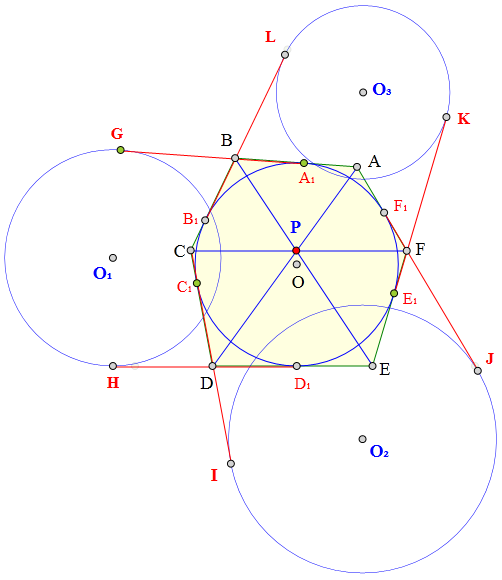
1.如图作切点A₁、B₁、C₁、D₁、E₁、F₁
2.延长A₁B到G,D₁D到H
延长C₁D到I,F₁F到J
延长B₁B到L,E₁F到K
使A₁G=D₁H=C₁I=F₁J=B₁L=E₁K
3.作⊙₁切AG于G,切EH于H
作⊙₂切CI于I,切AJ于J
作⊙₃切CL于L,切EK于K
由切线长定理易推出GB=BL,HE=KE,
所以BE为圆O1和圆O3的根轴,
同理可证CF为圆O2和圆O3的根轴,
AD为圆O1和圆O2的根轴,
由根心定理知,三个不在一条直线的三个圆的三条根轴必交于一点,
所以AD,BE,CF共点,
得证