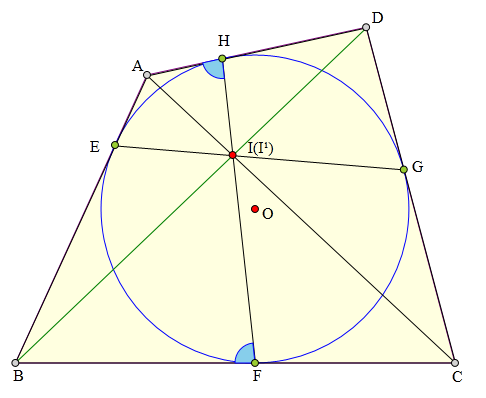
515 证明题:
⊙O内切四边形ABCD于:
E、F、G、H,求证:
AC、BD、EG、FH四线共点
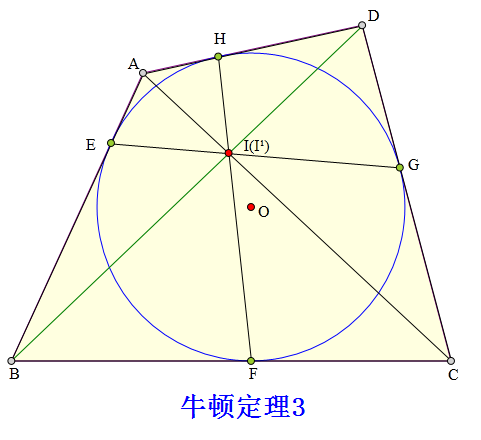
<解法 1:>
设EG、FH分别交AC于I、I¹,
易证:
∠AHI¹=∠BFI¹ ...(弦切角)
(AI¹·HI¹)/(FI¹·CI¹)
=S△AI¹H/S△CI¹F ...(sinx=sin(π-x))
=(AH·HI¹)/(CF·FI¹)
∴ AI'/CI'=AH/CF.
同样可证:AI/CI=AE/CG
又∵AE=AH,CF=CG.
∴AI/CI=AH/CF=AI'/CI'.
∴I,I'重合.
∴AC,EG,FH交于一点.
同理可证:直线BD,EG,FH交于一点.
∴ AC,BD,EG,FH交于一点。