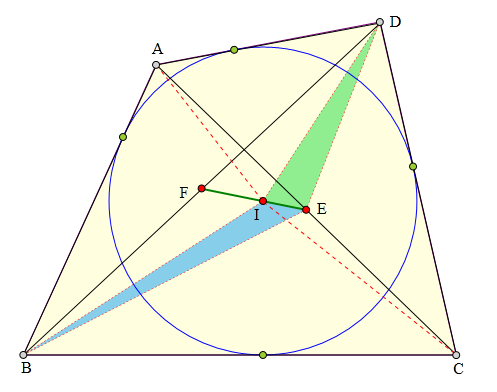
514 证明题:
四边形ABCD为⊙I外切圆,
E、F分别为AC、BD中点,
求证:
E、I、F三点共线。
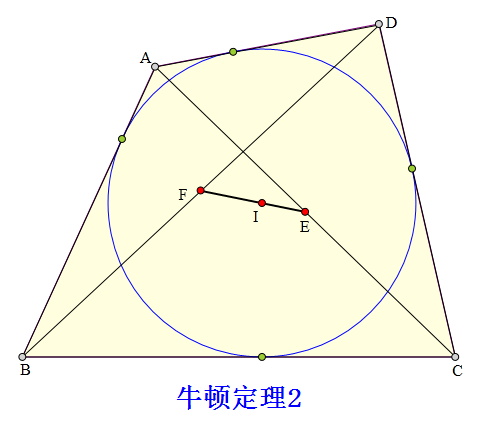
<解法 1:>
连接BI、BE、DI、DE、AI、CI,
易证:
S△BEI=S△BIC+S△CEI-S△BCE,
而S△DEI=S△ADE+S△AIE-S△AID。
∵AB+CD=AD+BC,
S△BIC+S△AID=½S□ABCD,
S△ADE+S△BCE
=½S△ACD+½S△ABC
=½S□ABCD
即S△BIC+S△AID=S△ADE+S△BCE,
移项得S△BIC-S△BCE=S△ADE-S△AID,
∵E是AC中点,
S△CEI=S△AEI,
∴S△BIC+S△CEI-S△BCE
=S△ADE+S△AIE-S△AID,
∴S△BEI=△DEI,
∵F是BD中点,
由共边比例定理得:
EI过点F即EF过点I,
故得证。