512 证明题:
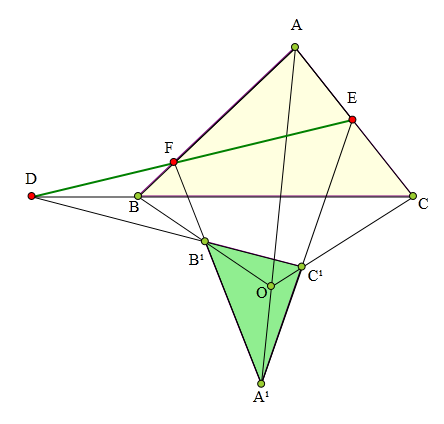
△ABC与△A¹B¹C¹中,
AA¹、BB¹、CC¹交于O,
BC、B¹C¹交于D,
AC、A¹C¹交于E,
AB、A¹B¹交于F,
求证D、E、F共线
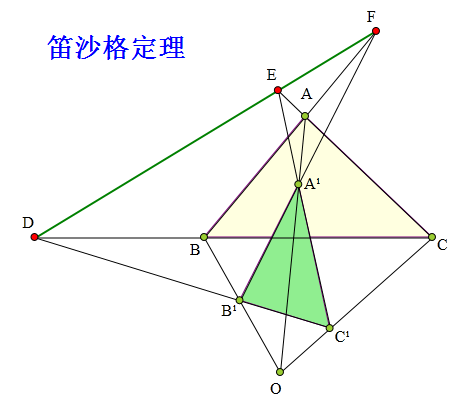
<解法 1:>
根据梅涅劳斯定理知:
DB¹C¹为△OBC和梅尼线,
∴(OB¹/B¹B)·(BD/DC)·(CC¹/C¹O)=1...①
同理:
∴(OA¹/A¹A)·(AF/FB)·(BB¹/B¹O)=1...②
∴(OC¹/C¹C)·(CE/EA)·(AA¹/A¹O)=1...③
①X②X③得:
(BD/DC)·(CE/EA)·(AF/FB)=1
根据梅涅劳斯逆定理知:
D、E、F共线