511 证明题:
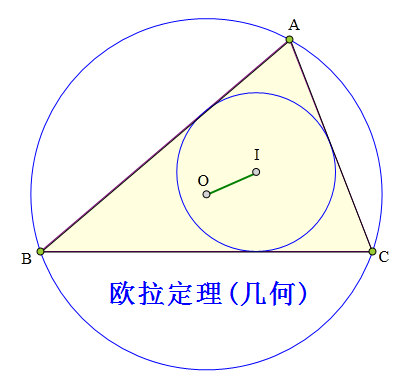
I、O分别为△ABC内心、外心。
⊙I、⊙O半径分别为r、R。
求证:
IO²=R²-2Rr
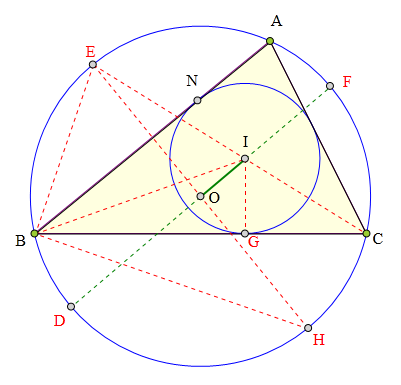
<解法 1:>
设IO=d
作IG丄BC于G
延长IO交⊙O于D、F
延长CI交⊙O于E
延长EO交⊙O于H
连接BE、BH、BI
则有:
R²-d²=(R+d)(R-d)=ID·IF
根据相交弦定理得:
ID·IF=IE·IC
∴R²-d²=IE·IC .........①
易证△IGC~△EBH
∴IC/EH=IG/BE
∴IC/2R=r/BE
∴2Rr=BE·IC
∵∠EBI=∠EBA+½∠ABC
=∠ECA+½∠ABC
=½∠ACB+½∠ABC
∠EIB=∠ICA+∠IBC
=½∠ACB+½∠ABC
∴∠EBI=∠EIB
∴BE=IE
∴2Rr=BE·IC=IE·IC .........②
由①②得:
2Rr=R²-d²
∴IO²=R²-2Rr