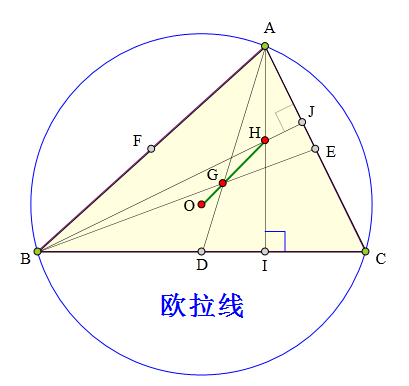
510 证明题:
H、G、O分别为△ABC的
垂心、重心、外心。
求证:
1. H、G、O三点共线
2. HG=2OG
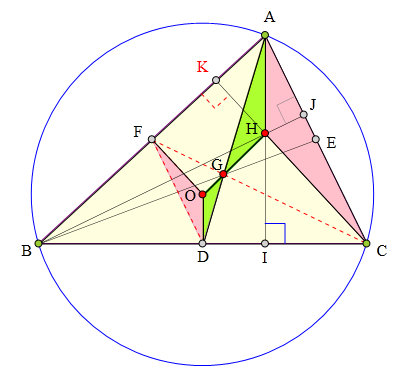
<解法 1:>
设D、E、F分别为BC、AC、AB的中点,
I、J、K分别为边BC、AC、AB上的垂足。
连接OD、OF、FD,易证:
OD//AI,DF//AC,∠ADO=∠DAI。
同理可证:∠OFC=∠FCK。
∴∠DFC=∠ACF, ∠FCA=∠CAD
∴∠OFD=∠HCA,∠ODF=∠HAC
∴△OFD~△HCA
∴AH:DO=AC:DF=2。
∵AG:GD=2
∴△GOD~△GAH
∴∠OGD=∠AGH
∴H、G、O三点共线且HG:GO=2