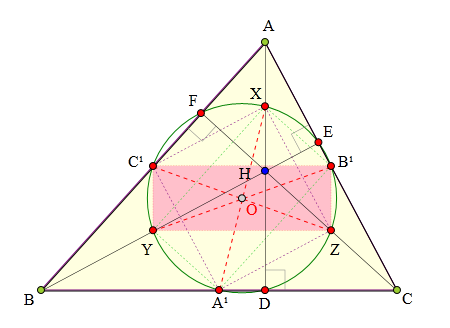
509 证明题:
H为△ABC垂心,
D、E、F分别为三边
BC、AC、AB上的垂足.
A¹、B¹、C¹分别为
BC、AB、AC的中点.
X、Y、X分别为
AH、BH、CH的中点.
求证:
A¹、B¹、C¹、
D、E、F、X、Y、Z
九点共圆.
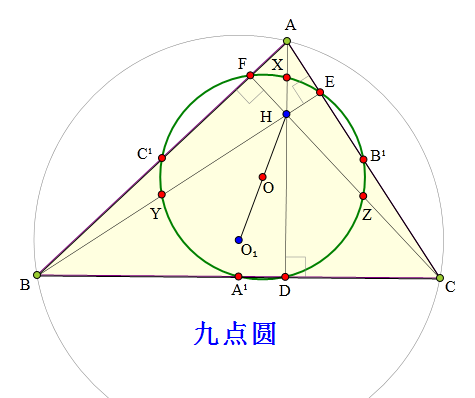
<解法 1:>
连接B¹、C¹、Y、Z,
由中位线及垂线易证
B¹C¹YZ为矩形...①
同理可证:
A¹C¹XZ为矩形...②
A¹B¹XY为矩形...③
∵矩形①②③两两共对角线
∴A¹、B¹、C¹、X、Y、Z六点共圆。
连接对角线A¹X,取其中点O,
则O为六点圆圆心。
∵△XDA¹为Rt△
∴D也在⊙O上
同理E、F也在⊙O上
∴A¹、B¹、C¹、X、Y、Z、D、E、F九点共圆