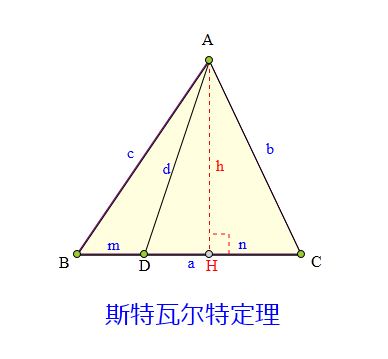
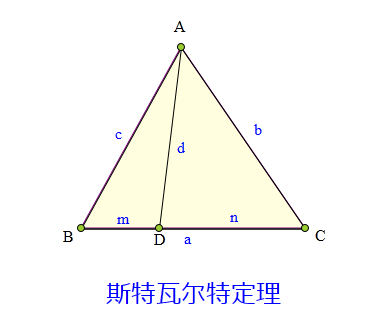
D为△ABC边BC上一点，
设AB=c, AC=b, BC=a,
AD=d, BD=m, DC=n。
求证：
nc²+mb²-ad² = amn

根据广勾股定理有：
b²=d²+n²-2n·DH ...①
斯特瓦尔特定理
斯特瓦尔特定理
c²=d²+m²+2m·DH ...②
用m乘①式两边得：
b²·m=d²·m+n²·m-2n·DH·m ...③
用n乘②式两边得：
c²·n=d²·n+m²·n+2m·DH·n ...④
由③+④得：
b²·m+c²·n
=d²·(m+n)+n²·m+m²·n
=d²·a+m·n·a
∴c²·n+b²·m-d²·a=a·n·m