502 证明题:
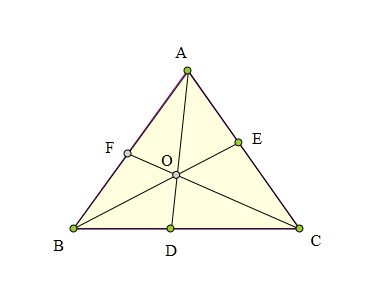
O为△ABC内一点,
AO交BC于D,
BO交AC于E,
CO交FB于F。
求证:
BD·CE·AF=DC·EA·FB
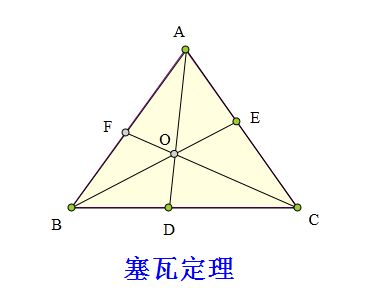
<解法 1:>
∵BD/DC=S△ABD/S△ACD
=S△BOD/S△COD
=(S△ABD-S△BOD)/(S△ACD-S△COD)
=S△AOB/S△AOC ...①
同理:
CE/EA=S△BOC/S△AOB ...②
AF/FB=S△AOC/S△BOC ...③
①×②×③得 :
(DB/CD)×(CE/EA)×(AF/FB)=1
∴BD·CE·AF=DC·EA·FB