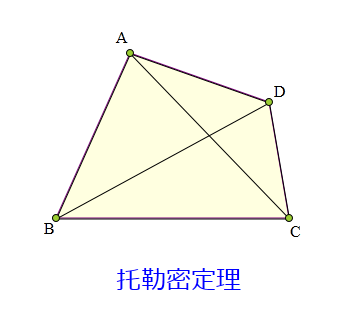
在四边形ABCD中，
求证：
①AB·CD+BC·AD≥AC·BD，
②当且仅当A、B、C、D
四点共圆时等式成立。

①
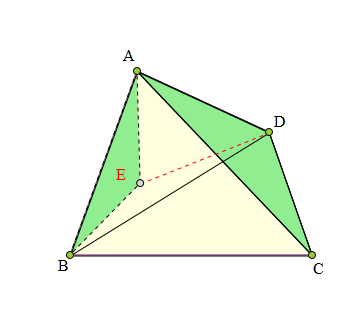
取四边形ABCD内一点E，
使得∠BAE=∠CAD，∠ABE=∠ACD。
则：△ABE～△ACD。
∴AB/AC=BE/CD
∴AB·CD=AC·BE
又∵AB/AC=AE/AD 且 ∠BAC=∠EAD。
∴△ABC～△AED。
∴BC/AC=ED/AD
∴AD·BC=AC·ED
∴AB·CE+AD·BC=AC·(BE+ED)
∴AB·CE+AD·BC≥AC·BD

②
若A、B、C、D四点共圆，
则 ∠ABE=∠ABD=∠ACD，
则 E在BD上，
则 BE+ED = BD，
则等式成立。
否则E在BD之外，
则BE+ED > BD