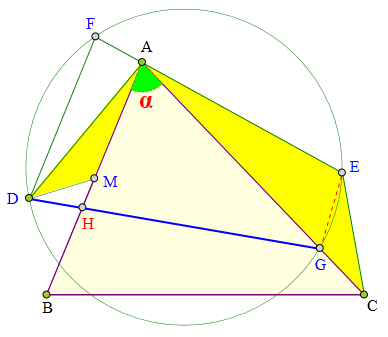
491 证明题:
D、E为△ABC外AB、AC侧一点,
M为AB中点,
△ADM~△ACE,
DF//AB交EA延长线于F,
⊙(DEF)交AC于G,
求证:
DG平分△ABC面积
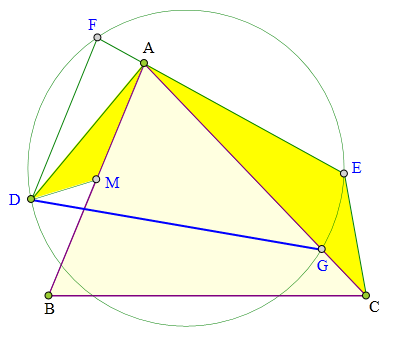
<解法 1:>
设DG交AB于H,∠BAC=α,
∵AH//DE,E、F、D、G共圆
∴∠AHD=∠AEG
又∵△ADM~△ACE
∴△AHD~△AEG
∴AD:AG=AH:AE,AD:AC=AM:AE
∴AD·AE=AG·AH=AC·AM=½AC·AB
∴AG·AH=½AC·AB
∴S△AGH=½AG·AH·sinα = ½S△ABC
得证