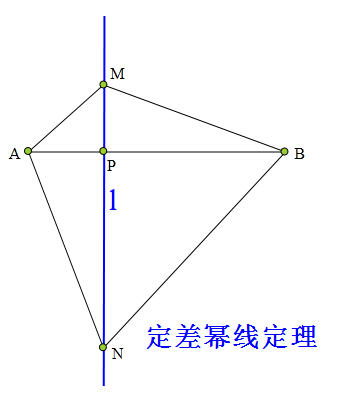
551 证明题:
直线l与AB交于P,
M、N为l上任意两点,
AM²-AN²=BM²-BN²,
求证:直线l⊥AB。
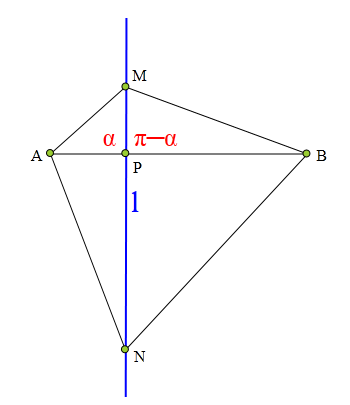
<解法 1:>
设∠APM=α,则∠BPM=π-α.
故AM²-AN²=AP²+MP²-2AP·MPcosα+2AP·NPcosα-AP²-NP²
=MP²-NP²-2AP·MPcosα+2AP·NPcosα.
BM²-BN²=MP²+BP²-2MP·BPcos(π-α)-NP²-BP²+2NP·BPcos(π-α).
=MP²-NP²+2MP·BPcosα-2NP·BPcosα.
由AM²-AN² = BM²-BN²得:
2AP·NPcosα-2AP·MPcosα=2MP·BPcosα-2NP·BPcosα,
即NP(AP+BP)cosα=MP(AP+BP)cosα.
∴(MP-NP)cosα=0,
∵(MP-NP)>0
∴cosα=0
∵0<α<π
∴α= π/2
故得证