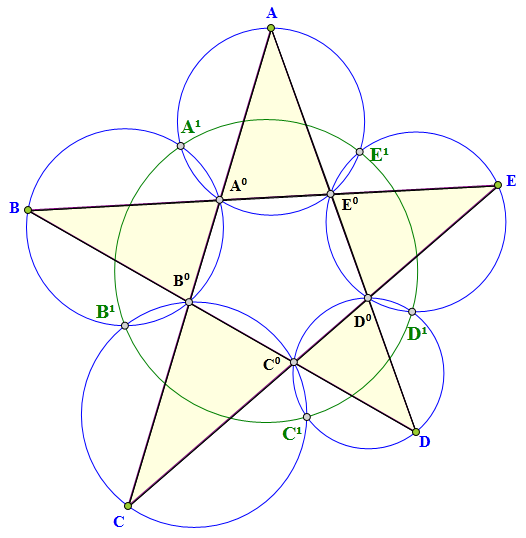
A、B、C、D、E为平面上五点，
AC交BE于A⁰，
BD交AC于B⁰，
CE交BD于C⁰，
AD交CE于D⁰，
EB交AD于E⁰，
△AA⁰E⁰、△BB⁰A⁰、△CC⁰B⁰、
△DD⁰C⁰、△EE⁰D⁰五个三角形
的外接圆的两两相交的
另一个交点分别为：
A¹、B¹、C¹、D¹、E¹。
求证：
A¹、B¹、C¹、D¹、E¹五点共圆。

①
连接B⁰C¹、C⁰C¹、C¹D，
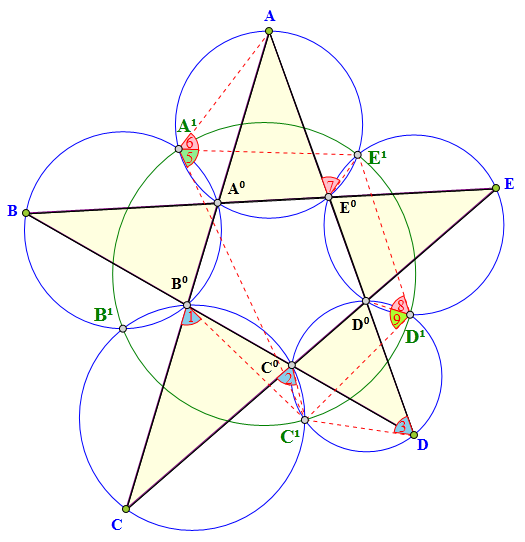
易知∠1=∠2=∠3,
∴AB⁰C¹D四点共圆
同理：AA¹B⁰D四点共圆
∴ADC¹A1四点共圆。

②
连接AA¹、A¹C¹、A¹E1、E⁰E¹、D¹E¹、C¹D¹、C⁰C¹。
易知∠5+∠6+∠3=180°，
∵∠6=∠7=∠8，∠9=∠3，
∴∠5+∠8+∠9=180°，
∴A¹、C¹、D¹、E¹四点共圆，
同理可证B¹、D¹、E¹、A¹四点共圆，
根据三角形外接圆只有一个可知
A¹、B¹、C¹、D¹、E¹四点共圆。